Bestimmung des Rückzahlungsplans, der periodische Zahlungen, der gesamten Rückzahlungssumme, oder
der Zinsraten kann etwas kompliziert sein. GnuCash hat einen eingebauten
Darlehensrechner, um diese Art von Berechnungen zu vereinfachen. Um
diesen Rechner aufzurufen, gehen Sie auf
→
.
Der Darlehensrechner kann dazu benutzt werden, aus jeweils vier bekannten Darlehensparametern jeden der Parameter zu berechnen: Zahlungsintervalle, Zinssatz, Aktueller Wert, Periodische Zahlungen, oder Zukünftiger Wert . Sie müssen auch die Zins- und die Zahlungsmodalitäten angeben.
Zahlungsintervalle – Die Anzahl der Zahlungsintervalle.
Zinssatz – Der Nominalzinssatz des Darlehens, bzw. der Jahreszinssatz.
Aktueller Wert- Der aktuelle Wert des Darlehens, beziehungsweise der augenblicklich geschuldete Geldbetrag des Darlehens.
Periodische Zahlung – Der pro Intervall zu zahlende Geldbetrag.
Zukünftiger Wert – Die zukünftige Darlehenssumme, beziehungsweise die Darlehenssumme die nach Ablauf aller Zahlungsintervalle noch geschuldet wird.
Zinstyp – Es gibt zwei Methoden der Verzinsung, schrittweise und kontinuierlich. Für eine schrittweise Verzinsung wählen Sie bitte die Häufigkeit von jährlich bis täglich.
Zahlungen – Hier können Sie auswählen, ob die Zahlungen am Anfang oder am Ende des Zahlungsintervalls erfolgen. Weiterhin können hier die Zahlungsintervalle im Bereich von jährlich bis täglich eingestellt werden. Sowohl Zahlungen am Beginn des Intervalls als auch Vorwegzahlungen und noch geschuldetes Geld werden bei der Zinsberechnung berücksichtigt.
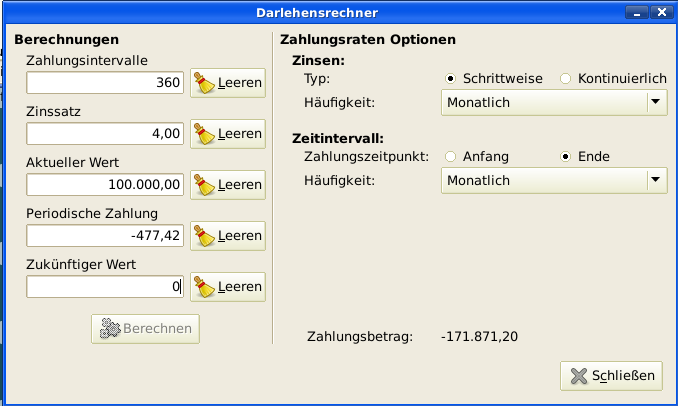
Wie hoch sind die monatlichen Raten für ein dreißigjähriges Darlehen von 100.000,- € bei einem festen Zinssatz von 4 % und monatlicher Verzinsung?
Dieses Szenario wird im obigen Beispielbild dargestellt. Um die Berechnungen durchzuführen, tragen Sie unter Zahlungsintervalle 360 ein (12 Monate mal 30 Jahre), Zinssatz auf 4, Aktueller Wert auf 100.000, lassen Sie Periodische Zahlung frei, und setzen Sie Zukünftiger Wert auf 0 (am Ende des Darlehens wollen Sie schuldenfrei sein). Die Verzinsung ist monatlich, die Zahlungen werden monatlich geleistet, unter der Annahme einer Zahlung am Ende des Intervalls und schrittweiser Verzinsung. Drücken Sie jetzt den Knopf unter den Darlehensparametern. Als Ergebnis sehen Sie -477,42 € im Feld periodische Zahlungen.
Antwort: die monatlichen Raten betragen -477,42 €
Wie lange dauert die Rückzahlung eines 22.000,- € Darlehen bei 10 % Zinssatz, monatlicher Verzinsung und einer Rückzahlung von 500,- € im Monat?
Zur Durchführung dieser Berechnungen lassen Sie Zahlungsintervalle frei, setzen den Zinssatz auf 10, Aktueller Wert auf20.000, Periodische Zahlung ist -500 und Zukünftiger Wert ist 0 (am Ende des Darlehens wollen Sie schuldenfrei sein). Verzinsung ist monatlich, Zahlungen sind monatlich, unter der Annahme einer Zahlung am Ende des Intervalls und schrittweiser Verzinsung. Drücken Sie jetzt den Knopf unter den Darlehensparametern. Als Ergebnis sehen Sie 49 im Feld Zahlungsintervalle.
Antwort: Die Rückzahlung des Darlehens dauert vier Jahre und einen Monat (49 Monate).
Für die Besprechungen der mathematischen Formeln, die durch den Darlehensrechner benutzt werden definieren wir erst die folgenden Variablen.
n == Anzahl der Zahlungsperioden %i == nominaler Zinssatz PV == aktueller Wert PMT == periodische Zahlungen FV == zukünftiger Wert CF == Zinsperiode pro Jahr PF == Zahlungsperiode pro Jahr Normale Werte für CF und PF sind: 1 == jährlich 2 == halbjährlich 3 == dreimal im Jahr 4 == vierteljährlich 6 == alle zwei Monate 12 == monatlich 24 == halb monatlich 26 == alle zwei Wochen 52 == wöchentlich 360 == täglich (12 x 30 Tage) 365 == täglich
Wenn eine Lösung für n, PV, PNT oder FV benötigt wird, muss zuerst der nominale Zinssatz (i) in den effektiven Zinssatz (ieff) für die Zahlungsperiode umgerechnet werden. Dieser effektive Zinssatz wird dann benutzt, um die gewünschte Variable zu berechnen. Wenn eine Lösung für i benötigt wird, ergibt die Berechnung den effektiven Zinssatz (ieff). Deshalb benötigen wir Funktionen, die den nominalen Zinssatz in den effektiven Zinssatz, und den effektiven Zinssatz in den Nominalzinssatz umrechnen.
Zur Umrechnung von i nach ieff werden folgende Formeln genutzt: schrittweise Verzinsung: ieff = (1 + i/CF)^(CF/PF) - 1 kontinuierliche Verzinsung: ieff = e^(i/PF) - 1 = exp(i/PF) - 1 Zur Umrechnung von ieff nach i werden folgende Formeln genutzt: schrittweise Verzinsung: i = CF*[(1+ieff)^(PF/CF) - 1] kontinuierliche Verzinsung: i = ln[(1+ieff)^PF]
 | Anmerkung |
|---|---|
In den unten stehenden Gleichungen für Geldgeschäfte sind alle Zinssätze die effektiven Zinssätze, „ieff“. Aus Gründen der Kürze wird statt „ieff“ nur „i“benutzt. | |
Eine Gleichung verbindet alle fünf genannten Variablen. Diese ist bekannt als die grundlegende Finanzgleichung:
PV*(1 + i)^n + PMT*(1 + iX)*[(1+i)^n - 1]/i + FV = 0
Dabei ist: X = 0 für Zahlungen am Ende des Zeitraums und
X = 1 für Zahlungen am Anfang des Zeitraums.Aus dieser Gleichung können Funktionen abgeleitet werden, um einzelne Variablen zu berechnen. Für
eine ausführliche Beschreibung der Ableitung dieser Gleichungen lesen Sie bitte die
Kommentare in der Datei src/calculation/fin.c im GnuCash Quelltext. Die Variablen A, B, und
C werden zuerst definiert, um die nachfolgenden Gleichungen übersichtlicher zu machen.
A = (1 + i)^n - 1 B = (1 + iX)/i C = PMT*B n = ln[(C - FV)/(C + PV)]/ln((1 + i) PV = -[FV + A*C]/(A + 1) PMT = -[FV + PV*(A + 1)]/[A*B] FV = -[PV + A*(PV + C)] Die Auflösung nach dem Zinssatz wird in zwei Fälle unterteilt. Der einfache Fall mit PMT == 0 ergibt die Gleichung: i = [FV/PV]^(1/n) - 1
Der Fall, wo PMT != 0 ist ziemlich komplex und wird hier nicht behandelt. Statt eine exakt lösbare Funktionen zur Bestimmung des Zinssatzes für den Fall PMT !=0 zu benutzen, wird ein interaktiver Prozess verwendet. Bitte lesen Sie die Datei src/calculation/fin.c für eine ausführliche Erklärung.
Jetzt wollen wir das Beispiel Abschnitt 8.3.1, „Beispiel: monatliche Zahlungen“, erneut berechnen, diesmal aber statt mit dem Darlehensrechner mit den vorgestellten mathematischen Formeln. Wie hoch sind die monatlichen Raten für ein dreißigjähriges Darlehen von 100.000 € bei einem festen Zinssatz von 4 % und monatlicher Verzinsung?
Zuerst wollen wir die Variablen bestimmen: n = (30*12) = 360, PV = 100000, PMT = unbekannt, FV = 0, i = 4%=4/100=0.04, CF = PF = 12, X = 0 (am Ende der Zahlungsintervalle).
Der zweite Schritt ist die Umwandlung des nominalen Zinssatzes (i) in den effektiven Zinssatz (ieff). Da der Zinssatz monatlich berechnet wird, haben wir schrittweise Verzinsung, und wir benutzen die Formel: ieff = (1 + i/CF)^(CF/PF) - 1, durch einsetzen der Werte ergibt sich ieff = (1 + 0.04/12)^(12/12) - 1, oder ieff = 1/300 = 0.0033333.
Jetzt können wir A und B berechnen. A = (1 + i)^n - 1 = (1 + 1/300)^360 - 1 = 2.313498. B = (1 + iX)/i = (1 + (1/300)*0)/(1/300) = 300.
Mit A und B können wir die PMT berechnen. PMT = -[FV + PV*(A + 1)]/[A*B] = -[0 + 100000*(2.313498 + 1)] / [2.313498 * 300] = -331349.8 / 694.0494 = -477.415296 = -477.42.
Antwort: die monatlichen Raten betragen 477,42 €.